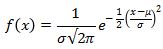Confidence Interval | Standard Deviation Tidak Diketahui

 

Memahami Apa itu Confidence Interval

Confidence Interval mengukur tingkat ketidakpastian atau kepastian dalam metode pengambilan sampel. Mereka dapat mengambil sejumlah batas probabilitas, dengan yang paling umum adalah tingkat kepercayaan 95% atau 99%. Confidence Interval dilakukan dengan menggunakan metode statistik, seperti uji-t.

Ahli statistik menggunakan Confidence Interval untuk mengukur ketidakpastian dalam variabel sampel. Misalnya, seorang peneliti memilih sampel yang berbeda secara acak dari populasi yang sama dan menghitung Confidence Interval untuk setiap sampel untuk melihat bagaimana hal itu dapat mewakili nilai sebenarnya dari variabel populasi. Kumpulan data yang dihasilkan semuanya berbeda; beberapa interval menyertakan parameter populasi sebenarnya dan yang lainnya tidak.Confidence Interval adalah rentang nilai, dibatasi di atas dan di bawah rata-rata statistik, yang kemungkinan akan berisi parameter populasi yang tidak diketahui. Tingkat kepercayaan mengacu pada persentase probabilitas, atau kepastian, bahwa Confidence Interval akan berisi parameter populasi sebenarnya ketika Anda menggambar sampel acak berkali-kali. Atau, dalam bahasa sehari-hari, “kami 99% yakin (tingkat kepercayaan) bahwa sebagian besar sampel ini (Confidence Interval) berisi parameter populasi yang sebenarnya.”

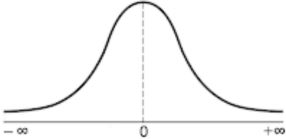
Kesalahpahaman terbesar mengenai Confidence Interval adalah bahwa mereka mewakili persentase data dari sampel tertentu yang berada di antara batas atas dan bawah. Misalnya, seseorang mungkin secara keliru menafsirkan Confidence Interval 99% yang disebutkan di atas dari 70 hingga 78 inci sebagai menunjukkan bahwa 99% data dalam sampel acak berada di antara angka-angka ini. Ini tidak benar, meskipun ada metode analisis statistik yang terpisah untuk membuat penentuan seperti itu. Melakukannya melibatkan mengidentifikasi mean dan standar deviasi sampel dan memplot angka-angka ini pada kurva lonceng.

Menghitung Confidence Interval

Misalkan sekelompok peneliti sedang mempelajari ketinggian pemain bola basket sekolah menengah. Para peneliti mengambil sampel acak dari populasi dan menetapkan tinggi rata-rata 74 inci.

Rata-rata 74 inci adalah perkiraan titik dari rata-rata populasi. Estimasi titik dengan sendirinya memiliki kegunaan yang terbatas karena tidak mengungkapkan ketidakpastian yang terkait dengan estimasi; Anda tidak memiliki pemahaman yang baik tentang seberapa jauh rata-rata sampel 74 inci ini dari rata-rata populasi. Apa yang hilang adalah tingkat ketidakpastian dalam sampel tunggal ini.

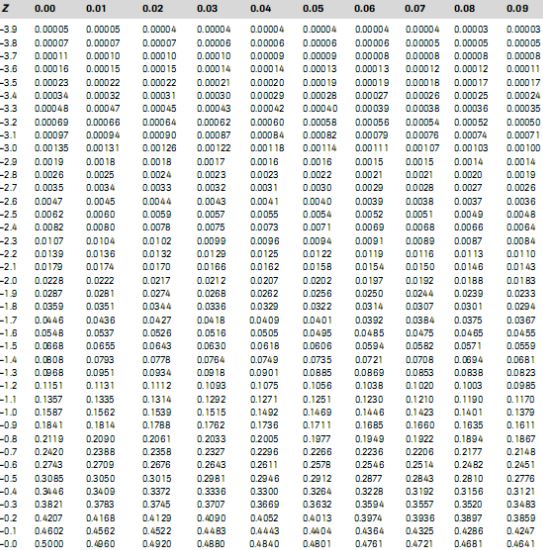
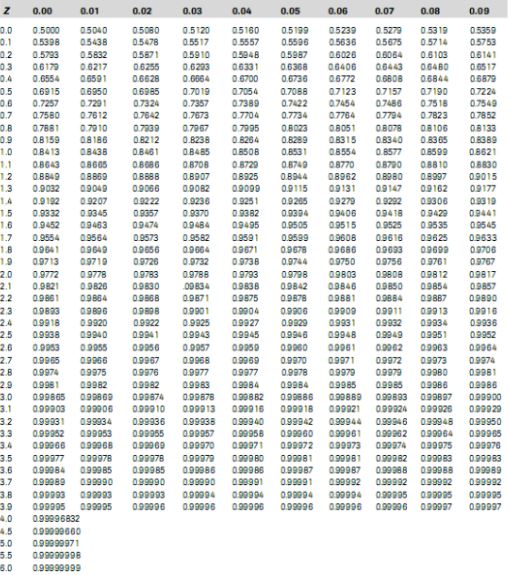
Confidence Interval memberikan lebih banyak informasi daripada perkiraan poin. Dengan menetapkan Confidence Interval 95% menggunakan rata-rata sampel dan standar deviasi, dan dengan asumsi distribusi normal seperti yang diwakili oleh kurva lonceng, para peneliti sampai pada batas atas dan bawah yang berisi rata-rata sebenarnya 95% dari waktu.Asumsikan intervalnya antara 72 inci dan 76 inci. Jika para peneliti mengambil 100 sampel acak dari populasi pemain bola basket sekolah menengah secara keseluruhan, rata-rata harus turun antara 72 dan 76 inci di 95 sampel tersebut.

Jika para peneliti menginginkan kepercayaan yang lebih besar, mereka dapat memperluas interval hingga kepercayaan 99%. Melakukan hal itu selalu menciptakan jangkauan yang lebih luas, karena memberikan ruang untuk jumlah sampel yang lebih banyak. Jika mereka menetapkan Confidence Interval 99% sebagai antara 70 inci dan 78 inci, mereka dapat mengharapkan 99 dari 100 sampel yang dievaluasi mengandung nilai rata-rata di antara angka-angka ini.

Tingkat kepercayaan 90%, di sisi lain, menyiratkan bahwa kita mengharapkan 90% dari perkiraan interval untuk memasukkan parameter populasi, dan seterusnya.

Apa yang bisa dilakukan dengan Confidence Interval?

Confidence Interval adalah rentang nilai, dibatasi di atas dan di bawah rata-rata statistik, yang kemungkinan akan berisi parameter populasi yang tidak diketahui. Tingkat kepercayaan mengacu pada persentase probabilitas, atau kepastian, bahwa Confidence Interval akan berisi parameter populasi sebenarnya ketika Anda menggambar sampel acak berkali-kali.

Bagaimana Confidence Interval Digunakan?

Ahli statistik menggunakan Confidence Interval untuk mengukur ketidakpastian dalam variabel sampel. Misalnya, seorang peneliti memilih sampel yang berbeda secara acak dari populasi yang sama dan menghitung Confidence Interval untuk setiap sampel untuk melihat bagaimana hal itu dapat mewakili nilai sebenarnya dari variabel populasi. Kumpulan data yang dihasilkan semuanya berbeda di mana beberapa interval menyertakan parameter populasi sebenarnya dan yang lainnya tidak.

Apa Kesalahpahaman Umum Tentang Confidence Interval?

Kesalahpahaman terbesar mengenai Confidence Interval adalah bahwa mereka mewakili persentase data dari sampel tertentu yang berada di antara batas atas dan bawah. Dengan kata lain, akan salah untuk mengasumsikan bahwa Confidence Interval 99% berarti bahwa 99% data dalam sampel acak berada di antara batas-batas ini. Apa artinya sebenarnya adalah bahwa seseorang dapat 99% yakin bahwa rentang tersebut akan berisi rata-rata populasi.

Apa itu Tes-T?

Confidence Interval dilakukan dengan menggunakan metode statistik, seperti uji-t. Uji-t adalah jenis statistik inferensial yang digunakan untuk menentukan apakah ada perbedaan yang signifikan antara rata-rata dua kelompok, yang mungkin terkait dengan fitur tertentu. Menghitung uji-t membutuhkan tiga nilai data kunci. Mereka termasuk perbedaan antara nilai rata-rata dari setiap kumpulan data (disebut perbedaan rata-rata), standar deviasi setiap kelompok, dan jumlah nilai data dari setiap kelompok.

Normal Approximation terhadap Binomial Distributions

 Apa Pendekatan Normal untuk Distribusi Binomial?

Variabel acak dengan distribusi binomial diketahui bersifat diskrit. Ini berarti bahwa ada sejumlah hasil yang dapat dihitung yang dapat terjadi dalam distribusi binomial, dengan pemisahan di antara hasil tersebut. Misalnya, variabel binomial dapat mengambil nilai tiga atau empat, tetapi bukan angka di antara tiga dan empat.

Dengan karakter diskrit dari distribusi binomial, agak mengejutkan bahwa variabel acak kontinu dapat digunakan untuk mendekati distribusi binomial. Untuk banyak distribusi binomial , kita dapat menggunakan distribusi normal untuk memperkirakan probabilitas binomial kita.

Hal ini dapat dilihat saat melihat lemparan koin n dan X adalah jumlah kepala. Dalam situasi ini, kami memiliki distribusi binomial dengan probabilitas keberhasilan sebagai p = 0,5. Saat kita meningkatkan jumlah lemparan, kita melihat bahwa histogram probabilitas memiliki kemiripan yang semakin besar dengan distribusi normal.

Pernyataan Pendekatan Normal

Setiap distribusi normal sepenuhnya ditentukan oleh dua bilangan real . Angka-angka ini adalah mean, yang mengukur pusat distribusi, dan deviasi standar , yang mengukur penyebaran distribusi. Untuk situasi binomial tertentu, kita perlu menentukan distribusi normal mana yang akan digunakan.

Pemilihan distribusi normal yang benar ditentukan oleh jumlah percobaan n dalam pengaturan binomial dan probabilitas konstan keberhasilan p untuk masing-masing percobaan ini. Perkiraan normal untuk variabel binomial kita adalah rata-rata np dan deviasi standar ( np (1 - p ) 0,5 .Misalnya, kita menebak masing-masing dari 100 pertanyaan tes pilihan ganda, di mana setiap pertanyaan memiliki satu jawaban yang benar dari empat pilihan. Jumlah jawaban benar X merupakan variabel acak binomial dengan n = 100 dan p = 0,25. Jadi variabel acak ini memiliki mean 100 (0,25) = 25 dan standar deviasi (100 (0,25) (0,75)) 0,5 = 4,33. Distribusi normal dengan mean 25 dan deviasi standar 4,33 akan bekerja untuk mendekati distribusi binomial ini.

Kapan Pendekatannya Sesuai?

Dengan menggunakan beberapa matematika dapat ditunjukkan bahwa ada beberapa kondisi yang kita perlukan untuk menggunakan pendekatan normal terhadap distribusi binomial . Jumlah pengamatan n harus cukup besar, dan nilai p sehingga np dan n (1 - p ) lebih besar dari atau sama dengan 10. Ini adalah aturan praktis, yang dipandu oleh praktik statistik. Pendekatan normal selalu dapat digunakan, tetapi jika kondisi ini tidak terpenuhi maka perkiraan tersebut mungkin tidak sebaik perkiraan.

Misalnya, jika n = 100 dan p = 0,25 maka kita dibenarkan menggunakan aproksimasi normal. Hal ini karena np = 25 dan n (1 - p ) = 75. Karena kedua bilangan ini lebih besar dari 10, distribusi normal yang sesuai akan cukup baik dalam memperkirakan probabilitas binomial.

Mengapa Menggunakan Approximation?

Probabilitas binomial dihitung dengan menggunakan rumus yang sangat mudah untuk mencari koefisien binomial. Sayangnya, karena faktorial dalam rumus, sangat mudah mengalami kesulitan komputasi dengan rumus binomial . Perkiraan normal memungkinkan kita untuk melewati salah satu masalah ini dengan bekerja dengan teman yang sudah dikenal, tabel nilai distribusi normal standar.

Seringkali penentuan probabilitas bahwa variabel acak binomial berada dalam kisaran nilai yang membosankan untuk dihitung. Ini karena untuk mencari probabilitas variabel binomial X lebih besar dari 3 dan kurang dari 10, kita perlu mencari probabilitas bahwa X sama dengan 4, 5, 6, 7, 8, dan 9, lalu menjumlahkan semua probabilitas ini. bersama. Jika aproksimasi normal dapat digunakan, kita perlu menentukan skor-z yang sesuai dengan 3 dan 10, dan kemudian menggunakan tabel probabilitas skor-z untuk distribusi normal standar .

variable pada normal distribution

Apa Itu Distribusi Normal?

Distribusi normal merupakan sebuah fungsi probabilitas yang menunjukkan distribusi atau penyebaran suatu variabel. Fungsi tersebut umumnya dibuktikan oleh sebuah grafik simetris yang disebut kurva lonceng (bell curve). Saat menandakan distribusi yang merata, kurva akan memuncak di bagian tengah dan melandai di kedua sisinya dengan nilai yang setara. 

Teori distribusi ini dikenal pula dengan istilah Distribusi Gauss (Gaussian Distribution). Istilah tersebut mengacu pada Carl Friedrich Gauss, seorang matematikawan asal Jerman yang mengembangkan teori distribusi berisi fungsi eksponensial dua parameter pada periode 1794-1809. Meski demikian, teori awal yang menjadi cikal-bakal fungsi distribusi tersebut sebenarnya mulai dikembangkan oleh Abraham de Moivre pada tahun 1733.

Parameter Distribusi Normal

Seperti halnya teori distribusi lain dalam statistika probabilitas, bentuk kurva serta nilai peluang distribusi normal ditentukan oleh sejumlah parameter. Untuk distribusi ini, terdapat dua jenis parameter yang dijadikan acuan, yakni mean (nilai rata-rata) serta standar deviasi atau simpangan baku.

• Nilai rata-rata digunakan sebagai pusat distribusi atau penyebaran nilai lainnya. Nilai tersebut akan menentukan lokasi titik puncak dalam kurva lonceng, sedangkan nilai-nilai lainnya akan menyebar mengikuti rerata.
• Standar deviasi adalah penghitungan variabilitas yang menentukan lebar sebuah kurva distribusi normal. Standar ini dapat menghitung seberapa jauh kecenderungan data akan melebar dari nilai rata-rata yang menjadi titik pusatnya. Semakin kecil nilai standar deviasi, maka kurva akan berbentuk semakin runcing. Selain itu, standar deviasi juga menggambarkan jarak atau selisih umum antara mean dengan data lain yang diobservasi. 

Karakteristik Distribusi Normal

Saat menunjukkan nilai penyebaran data, distribusi normal memiliki sejumlah karakteristik utama sebagai berikut:

• Teori distribusi ini memiliki nilai mean, median, dan modus yang sama. Oleh karena itu, distribusinya sering pula disebut unimodal. 
• Kurva distribusi selalu bersifat simetris dengan bentuk lonceng (bell curve). Titik puncak kurva adalah nilai rata-rata. Nilai ini berada tepat di tengah kurva, sedangkan data distribusi terletak di sekitar garis lurus yang ditarik ke bawah dari titik tengah tersebut.
• Mean (nilai rata-rata) dan nilai standar deviasi akan menentukan bentuk dan lokasi distribusi.
• Jumlah luas daerah di bawah kurva normal bernilai 1, yakni ½ di sisi kiri dan ½ di sisi kanan. Hal ini juga berlaku untuk seluruh distribusi probabilitas kontinu.
• Dalam kurva distribusi, dapat disimpulkan jika setengah data populasi akan memiliki nilai yang kurang dari angka rata-rata, sedangkan sebagian lagi memiliki nilai yang lebih besar.
• Masing-masing ekor kurva di kedua sisi memanjang tak berbatas. Dalam beberapa kasus penghitungan distribusi, ekor kurva bahkan bisa memotong sumbu horizontal.

Kesimpulan: Seberapa Penting Distribusi Normal dalam Statistika?

Setelah mengetahui parameter dan karakteristik utama dalam teori distribusi normal, dapat disimpulkan jika teori ini memiliki posisi penting dalam konsep statistika peluang. Penerapan distribusi Gauss dianggap penting karena beberapa alasan berikut:

1. Dapat meningkatkan objektivitas penilaian. Hal ini sangat membantu dalam menempatkan anggota-anggota yang paling tepat untuk suatu kelompok tertentu, misalnya ketika mengevaluasi nilai siswa atau mengelompokkan pegawai dalam satu kriteria yang sama.
2. Dapat menghindari terjadinya bias atau penilaian yang condong pada satu kategori saja. Dengan distribusi yang simetris dan berpusat pada nilai rata-rata seluruh data dalam suatu populasi, penilaian yang berat sebelah atau tidak seimbang akan dapat dihindarkan.
3. Dapat membantu menentukan tingkat normalitas dan kecenderungan sentral. Dalam statistika, khususnya statistika peluang, normalitas suatu data adalah hal penting yang tidak boleh diabaikan. Melalui teori yang diterapkan oleh distribusi Gauss, kecenderungan sentral atau tingkat normalitas data dapat ditentukan secara lebih mudah. 

Demikian informasi mengenai distribusi normal serta parameter dan karakteristik yang melengkapi penerapannya. Bagi Anda yang tengah mempelajari statistika peluang atau sedang mencari teori pendukung dalam penghitungan data, informasi di atas bisa dijadikan salah satu referensi.

Kembangkan Dana Sekaligus Berikan Kontribusi Untuk Ekonomi Nasional dengan Melakukan Pendanaan Untuk UKM Bersama Akseleran!

Bagi kamu yang ingin membantu mengembangkan usaha kecil dan menengah di Indonesia, P2P Lending dari Akseleran adalah tempatnya. Sebagai platform pengembangan dana yang optimal dengan bunga hingga 21% per tahun kamu dapat memulainya hanya dengan Rp100 ribu saja.

Normal Distributions & Standard Normal Distributions

Lebih Dalam Mengenal Distribusi Normal dalam Statistik

Dalam teori distribusi peluang atau probabilitas, distribusi normal menempati posisi penting pada berbagai analisis statistika. Jenis distribusi ini juga digunakan sebagai acuan untuk menghitung beberapa fenomena yang sering ditemui dalam kehidupan sehari-hari. Penghitungan tekanan darah, tinggi badan, penghitungan kesalahan (error measurement), hingga penjabaran nilai IQ adalah beberapa kasus yang menggunakan distribusi normal sebagai acuan utamanya.

Apa Itu Distribusi Normal?

Distribusi normal merupakan sebuah fungsi probabilitas yang menunjukkan distribusi atau penyebaran suatu variabel. Fungsi tersebut umumnya dibuktikan oleh sebuah grafik simetris yang disebut kurva lonceng (bell curve). Saat menandakan distribusi yang merata, kurva akan memuncak di bagian tengah dan melandai di kedua sisinya dengan nilai yang setara. 

Teori distribusi ini dikenal pula dengan istilah Distribusi Gauss (Gaussian Distribution). Istilah tersebut mengacu pada Carl Friedrich Gauss, seorang matematikawan asal Jerman yang mengembangkan teori distribusi berisi fungsi eksponensial dua parameter pada periode 1794-1809. Meski demikian, teori awal yang menjadi cikal-bakal fungsi distribusi tersebut sebenarnya mulai dikembangkan oleh Abraham de Moivre pada tahun 1733.

Parameter Distribusi Normal

Seperti halnya teori distribusi lain dalam statistika probabilitas, bentuk kurva serta nilai peluang distribusi normal ditentukan oleh sejumlah parameter. Untuk distribusi ini, terdapat dua jenis parameter yang dijadikan acuan, yakni mean (nilai rata-rata) serta standar deviasi atau simpangan baku.

• Nilai rata-rata digunakan sebagai pusat distribusi atau penyebaran nilai lainnya. Nilai tersebut akan menentukan lokasi titik puncak dalam kurva lonceng, sedangkan nilai-nilai lainnya akan menyebar mengikuti rerata.
• Standar deviasi adalah penghitungan variabilitas yang menentukan lebar sebuah kurva distribusi normal. Standar ini dapat menghitung seberapa jauh kecenderungan data akan melebar dari nilai rata-rata yang menjadi titik pusatnya. Semakin kecil nilai standar deviasi, maka kurva akan berbentuk semakin runcing. Selain itu, standar deviasi juga menggambarkan jarak atau selisih umum antara mean dengan data lain yang diobservasi. 

Karakteristik Distribusi Normal

Saat menunjukkan nilai penyebaran data, distribusi normal memiliki sejumlah karakteristik utama sebagai berikut:

• Teori distribusi ini memiliki nilai mean, median, dan modus yang sama. Oleh karena itu, distribusinya sering pula disebut unimodal. 
• Kurva distribusi selalu bersifat simetris dengan bentuk lonceng (bell curve). Titik puncak kurva adalah nilai rata-rata. Nilai ini berada tepat di tengah kurva, sedangkan data distribusi terletak di sekitar garis lurus yang ditarik ke bawah dari titik tengah tersebut.
• Mean (nilai rata-rata) dan nilai standar deviasi akan menentukan bentuk dan lokasi distribusi.
• Jumlah luas daerah di bawah kurva normal bernilai 1, yakni ½ di sisi kiri dan ½ di sisi kanan. Hal ini juga berlaku untuk seluruh distribusi probabilitas kontinu.
• Dalam kurva distribusi, dapat disimpulkan jika setengah data populasi akan memiliki nilai yang kurang dari angka rata-rata, sedangkan sebagian lagi memiliki nilai yang lebih besar.
• Masing-masing ekor kurva di kedua sisi memanjang tak berbatas. Dalam beberapa kasus penghitungan distribusi, ekor kurva bahkan bisa memotong sumbu horizontal.

Kesimpulan: Seberapa Penting Distribusi Normal dalam Statistika?

Setelah mengetahui parameter dan karakteristik utama dalam teori distribusi normal, dapat disimpulkan jika teori ini memiliki posisi penting dalam konsep statistika peluang. Penerapan distribusi Gauss dianggap penting karena beberapa alasan berikut:

1. Dapat meningkatkan objektivitas penilaian. Hal ini sangat membantu dalam menempatkan anggota-anggota yang paling tepat untuk suatu kelompok tertentu, misalnya ketika mengevaluasi nilai siswa atau mengelompokkan pegawai dalam satu kriteria yang sama.
2. Dapat menghindari terjadinya bias atau penilaian yang condong pada satu kategori saja. Dengan distribusi yang simetris dan berpusat pada nilai rata-rata seluruh data dalam suatu populasi, penilaian yang berat sebelah atau tidak seimbang akan dapat dihindarkan.
3. Dapat membantu menentukan tingkat normalitas dan kecenderungan sentral. Dalam statistika, khususnya statistika peluang, normalitas suatu data adalah hal penting yang tidak boleh diabaikan. Melalui teori yang diterapkan oleh distribusi Gauss, kecenderungan sentral atau tingkat normalitas data dapat ditentukan secara lebih mudah. 

Demikian informasi mengenai distribusi normal serta parameter dan karakteristik yang melengkapi penerapannya. Bagi Anda yang tengah mempelajari statistika peluang atau sedang mencari teori pendukung dalam penghitungan data, informasi di atas bisa dijadikan salah satu referensi.

Kembangkan Dana Sekaligus Berikan Kontribusi Untuk Ekonomi Nasional dengan Melakukan Pendanaan Untuk UKM Bersama Akseleran!

Bagi kamu yang ingin membantu mengembangkan usaha kecil dan menengah di Indonesia, P2P Lending dari Akseleran adalah tempatnya. Sebagai platform pengembangan dana yang optimal dengan bunga hingga 21% per tahun kamu dapat memulainya hanya dengan Rp100 ribu saja.

probabilitas pada distribusi normal

 Distribusi normal merupakan sebuah fungsi probabilitas yang menunjukkan distribusi atau penyebaran suatu variabel. Fungsi tersebut umumnya dibuktikan oleh sebuah grafik simetris yang disebut kurva lonceng (bell curve). ... Teori distribusi ini dikenal pula dengan istilah Distribusi Gauss (Gaussian Distribution)

Pengertian Distribusi Normal

Apa itu distribusi normal?

Distribusi normal merupakan salah satu jenis distribusi dengan variabel acak yang kontinu.

Pada distribusi normal terdapat kurva/grafik yang digambarkan menyerupai bentuk lonceng.

Distribusi normal dapat disebut juga sebagai distribusi Gauss. Persamaan yang terdapat dalam distribusi normal salah satunya yaitu terkait fungsi densitas.

Berikut merupakan fungsi densitas pada distribusi normal.

Rumus Distribusi Normal

Keterangan:

• π : konstanta dengan nilai 3,14159. . .
• e  : bilangan eksponensial dengan nilai 2,7183 . . .
• µ  : rata-rata (mean) dari data
• σ  : simpangan baku data berdistribusi normal

Bagaimana cara untuk menghitung nilai z? Nilai z dapat dihitung dengan rumus berikut.

z = (x – µ)/σ

Keterangan:

• µ  : rata-rata (mean) dari data
• σ  : simpangan baku data berdistribusi normal

Pada bagian sebelumnya dijelaskan bahwa data yang berdistribusi normal memiliki kurva yang berbentuk menyerupai lonceng.

Bentuk kurva dari data berdistribusi normal yaitu sebagai berikut.

Kurva distribusi normal

Berdasarkan kurva distribusi normal di atas, distribusi normal memiliki rata-rata (mean) sama dengan 0 dan simpangan baku sama dengan 1.

Berikut ini akan dijelaskan mengenai beberapa contoh penerapan distribusi normal.

Penerapan Distribusi Normal

Distribusi normal sangat penting untuk dipelajari terutama dalam melakukan analisis data statistika.

Dengan data yang diambil secara acak dan berdistribusi normal akan memudahkan dalam melakukan analisis dan meramalkan serta mengambil kesimpulan untuk cakupan yang lebih luas.

Distribusi normal banyak diterapkan dalam berbagai perhitungan statistika dan pemodelan yang berguna dalam berbagai bidang.

Dalam menentukan distribusi probabilitas diperlukan tabel z dari distribusi normal.

Tabel Z Distribusi Normal

Berikut merupakan tabel nilai z pada data yang berdistribusi normal.

Tabel Z distribusi normal

Pada tabel di atas terdapat acuan pada baris dan kolomnya. Hal tersebut untuk memudahkan dalam menentukan nilai z.

Berikut langkah-langkah dalam menentukan nilai z.

1. Perhatikan pada bagian kolom awal. Misalkan kita akan menentukan nilai untuk 1,56. Maka langkah pertama kita mencari pada baris 1,5.
2. Perhatikan pada baris awal. Carilah nilai 0,06.
3. Tentukan titik temu (sel) dari baris dan kolom yang dimaksud. Nilai z untuk 1,56 adalah 0,9406.

Berikut merupakan contoh soal terkait distribusi kelompok untuk meningkatkan pemahaman kalian.

Contoh Soal Distribusi Kelompok

Dalam suatu ujian terdapat 300 siswa yang mengikuti ujian tersebut. Rata-rata dari hasil ujian yaitu 70 serta simpangan baku hasil ujian tersebut adalah 10.

Jika data nilai hasil ujian siswa tersebut berdistribusi normal, maka berapa persen mahasiswa yang mendapat nilai A jika syarat untuk mendapatkan nilai A adalah nilai lebih dari 85.

Pembahasan

Berdasarkan contoh soal di atas, diperoleh informasi sebagai berikut.

µ  = 70

σ  = 10

x  = 85

akan ditentukan Z(X>85).

Z(X > 85) = 1 – Z(X < 85)

Akan dihitung terlebih dahulu nilai dari Z (X < 85)

Z = (85 – 70)/10 = 15/10 = 1,5

Nilai Z untuk 1,50 adalah 0,9332, sehingga

Z(X > 85) = 1 – Z(X < 85)

Z(X > 85) = 1 – 0,9332

Z(X > 85) = 0,0668

Z(X > 85) = 6,68%

Mari kita simpulkan materi mengenai distribusi normal.

Kesimpulan

Distribusi normal merupakan salah satu jenis distribusi dengan variabel acak yang kontinu. Pada distribusi normal terdapat kurva/grafik yang digambarkan menyerupai bentuk lonceng.

Untuk menentukan nilai z atau z-score  dapat digunakan rumus berikut.

z = (x – µ)/σ

Tabel nilai z pada distribusi normal digunakan untuk mempermudah dalam menentukan z-score.

Demikian pembahasan pada artikel dengan judul “Distribusi Normal”, semoga artikel ini dapat berguna bagi kalian dalam mempelajari materi statistika selanjutnya. Terima kasih. Baca juga Turunan.

distribusi geometrik & distribusi poisson

Distribusi ini pertama kali diperkenalkan oleh Siméon-Denis Poisson (1781–1840) dan diterbitkan, bersama teori probabilitasnya, pada tahun 1838 dalam karyanyaRecherches sur la probabilité des jugements en matière criminelle et en matière civile (“Penelitian Probabilitas Hukum Masalah Pidana dan Perdata”). Karyanya memfokuskan peubah acak N yang menghitung antara lain jumlah kejadian diskret (kadang juga disebut "kedatangan") yang terjadi selama interval waktu tertentu.

Apabila nilai harapan kejadian pada suatu interval adalah ${\displaystyle \lambda }$, maka probabilitas terjadi peristiwa sebanyak k kali (k adalah bilangan bulat non negatif, k = 0, 1, 2, ...) maka sama dengan

${\displaystyle f(k;\lambda )={\frac {\lambda ^{k}e^{-\lambda }}{k!}},\,\!}$

dimana

• e adalah basis logaritma natural (e = 2.71828...)
• k adalah jumlah kejadian suatu peristiwa  — peluang yang diberikan oleh fungsi ini
• k! adalah faktorial dari k
• λ adalah bilangan riil positif, sama dengan nilai harapan peristiwa yang terjadi dalam interval tertentu. Misalnya, peristiwa yang terjadi rata-rata 4 kali per menit, dan akan dicari probabilitas terjadi peristiwa k kali dalam interval 10 menit, digunakan distribusi Poisson sebagai model dengan λ = 10×4 = 40.

Sebagai fungsi k, ini disebut fungsi massa probabilitas. Distribusi Poisson dapat diturunkan sebagai kasus terbatas distribusi binomial. Distribusi Poisson dapat diterapkan pada sistem dengan kejadian berjumlah besar yang yang mungkin terjadi, yang mana kenyataannya cukup jarang. Contoh klasik adalah peluruhan nuklir atom.

permutasi dan kombinasi dengan phyton

Permutasi dan Kombinasi dengan Python

Permutasi dan Kombinasi dengan Python

Import Module

In [1]:

import itertools

Permutasi Sederhana

nPn=n!${}_n{P}_n=n!$

In [2]:

data = ['A', 'B', 'C']
permutasi = itertools.permutations(data)

for perm in permutasi:
    print(perm)

('A', 'B', 'C')
('A', 'C', 'B')
('B', 'A', 'C')
('B', 'C', 'A')
('C', 'A', 'B')
('C', 'B', 'A')

Permutasi pada sejumlah objek tertentu

nPr=n!(n−r)!${}_n{P}_r=\frac{n!}{(n-r)!}$

In [3]:

data = ['A', 'B', 'C', 'D']

4P2=4!(4−2)!=4×3×2!2!=12${}_4{P}_2=\frac{4!}{(4-2)!}=\frac{4\times 3\times 2!}{2!}=12$

In [4]:

permutasi = itertools.permutations(data, 2)

for perm in permutasi:
    print(perm)

('A', 'B')
('A', 'C')
('A', 'D')
('B', 'A')
('B', 'C')
('B', 'D')
('C', 'A')
('C', 'B')
('C', 'D')
('D', 'A')
('D', 'B')
('D', 'C')

Kalkulasi Permutasi dengan Python

kasus 1:

4P2=?${}_4{P}_2=?$

In [5]:

permutasi = itertools.permutations(range(4), 2)
len(tuple(permutasi))

Out[5]:

12

kasus 2:

10P4=?${}_{10}{P}_4=?$

In [6]:

permutasi = itertools.permutations(range(10), 4)
len(tuple(permutasi))

Out[6]:

5040

kasus 3:

43P3=?${}_{43}{P}_3=?$

In [7]:

permutasi = itertools.permutations(range(43), 3)
len(tuple(permutasi))

Out[7]:

74046

Kombinasi Sederhana

nCr=n!(n−r)!×r!${}_n{C}_r=\frac{n!}{(n-r)!\times r!}$

In [8]:

data = ['A', 'B', 'C', 'D', 'E']

5C3=5!(5−3)!×3!=5!2!×3!=10${}_5{C}_3=\frac{5!}{(5-3)!\times 3!}=\frac{5!}{2!\times 3!}=10$

In [9]:

kombinasi = itertools.combinations(data, 3)

for comb in kombinasi:
    print(comb)

('A', 'B', 'C')
('A', 'B', 'D')
('A', 'B', 'E')
('A', 'C', 'D')
('A', 'C', 'E')
('A', 'D', 'E')
('B', 'C', 'D')
('B', 'C', 'E')
('B', 'D', 'E')
('C', 'D', 'E')

Kalkulasi Kombinasi dengan Python

kasus 1:

5C3=?${}_5{C}_3=?$

In [10]:

kombinasi = itertools.combinations(range(5), 3)
len(tuple(kombinasi))

Out[10]:

10

kasus 2:

16C4=?${}_{16}{C}_4=?$

In [11]:

kombinasi = itertools.combinations(range(16), 4)
len(tuple(kombinasi))

Out[11]:

1820

Kombinasi lanjutan

Sebuah ember berisikan kelereng sebagai berikut: 4 kelereng merah, 3 kelereng biru, 4 kelereng hijau, dan 3 kelereng kuning.

pertanyaan:

1. berapa set/grup yang dapat dibentuk dari 4 kelereng?
2. berapa set/grup yang dapat dibentuk dari 4 kelereng jika tiap kelereng warnanya berbeda?
3. berapa set/grup yang dapat dibentuk dari 4 kelereng jika minimal terdapat 2 kelereng merah didalamnya?
4. berapa set/grup yang dapat dibentuk dari 4 kelereng jika warna merah tidak boleh diikut sertakan didalam set/grup, tetapi minimal harus ada 1 kelereng hijau?

In [12]:

data = ['m1','m2','m3','m4',
        'b1','b2','b3',
        'h1','h2','h3','h4',
        'k1','k2','k3']
data

Out[12]:

['m1',
 'm2',
 'm3',
 'm4',
 'b1',
 'b2',
 'b3',
 'h1',
 'h2',
 'h3',
 'h4',
 'k1',
 'k2',
 'k3']

jawaban no 1

In [13]:

kombinasi = itertools.combinations(data, 4)
len(tuple(kombinasi))

Out[13]:

1001

jawaban no 2

In [14]:

m = len(tuple(itertools.combinations(range(4),1)))
b = len(tuple(itertools.combinations(range(3),1)))
h = len(tuple(itertools.combinations(range(4),1)))
k = len(tuple(itertools.combinations(range(3),1)))
jawab = m * b * h * k
jawab

Out[14]:

144

jawaban no 3

In [15]:

# kondisi 1 = (2 merah dari 4 merah) * (2 bukan merah dari 10 bukan merah)
k1 = len(tuple(itertools.combinations(range(4),2))) * len(tuple(itertools.combinations(range(10),2)))

# kondisi 2 = (3 merah dari 4 merah) * (1 bukan merah dari 10 bukan merah)
k2 = len(tuple(itertools.combinations(range(4),3))) * len(tuple(itertools.combinations(range(10),1)))

# kondisi 3 = keempatnya merah

k3 = len(tuple(itertools.combinations(range(4),4)))

jawab = k1 + k2 + k3
jawab

Out[15]:

311

jawaban no 4

In [16]:

#kondisi 1 = 1h (1 hijau) * 3sh (3 selain hijau):tanpa merah
#kondisi 2 = 2h * 2sh: tanpa merah
#kondisi 3 = 3h * 1sh: tanpa merah
#kondisi 4 = 4h
#jawab = k1 + k2 + k3 + k4

k1 = len(tuple(itertools.combinations(range(4),1))) * len(tuple(itertools.combinations(range(6),3)))
k2 = len(tuple(itertools.combinations(range(4),2))) * len(tuple(itertools.combinations(range(6),2)))
k3 = len(tuple(itertools.combinations(range(4),3))) * len(tuple(itertools.combinations(range(6),1)))
k4 = len(tuple(itertools.combinations(range(4),4)))
jawab = k1 + k2 + k3 + k4
jawab

Out[16]:

195